چکيده:
نحوه ی مدلسازی تاير خودرو ، بدست آوردن نیروها و گشتاورهای بین تایر و زمین دارای نقش حیاتی در سیستم های هدایت و کنترل خودرو، از قبیل سیستم ترمز ضد قفل(ABS)، سیستم کنترل کشش خودرو (TCS) و… می باشد. بسیاری از کنترلرها به منظور کنترل ضریب اصطکاک بین تایر و زمین و تولید حداکثر نیروهای طولی وجانبی بوسیله تایر طراحی شده اند. انتخاب روش مناسب برای مدلسازی رفتار تایر از ضروریات طراحی کنترل کننده ی سیستم های هدایت و کنترل خودرو به شمار می آید. دراین مقاله ابتدا مدل های موجود تایر و زمین معرفی شده است. سپس ویژگی های هر مدل مورد بررسی قرار گرفته و با مقایسه نتایج بدست آمده، خصوصیات ویژه و تاثیر گذار هر مدل تحلیل شده است.
مقدمه:
تولید تایر خودرو قدمتی بالغ بر یک قرن دارد. در یکصد سال گذشته، صنعتگران و پژوهشگران کوشیده اند تا با تکامل ساختار تایر، به سهم خود، امکان توسعه هرچه بیشتر صنایع خودرو سازی را فراهم نمایند. در دهه 40 قرن بیستم، ایده ساخت یک محفظه لاستیکی در برگیرنده و حافظ هوای داخل تایر مطرح شد، که بعدها به تیوپ معروف گردید. از سال1947 اقدام به ساخت تایرهایی شد که در آنها از تیوپ استفاده نمی شد و به تایر های تیوب لس شهرت یافتند که تا به امروز مورد استفاده قرار گرفته اند و تلاش برای تولید تایرهای مقاوم تر، سبک تر، با عملکرد مکانیکی و حرکتی بهتر و مطلوب تر در راستای نیل به افزایش پایداری خودرو و کاهش نیروهای مقاوم تایر ادامه دارد.[1] [1][2] تایر در خودرو به عنوان تنها محل تماس خودرو به زمین، نقش بسزایی در راحتی سرنشین، پایداری و کنترل خودرو دارا می باشد. از طرفی مهمترین نقطه اشتراک سیستم های ترمز، فرمان، تعلیق و انتقال قدرت خودرو، تایر می باشد. ضمن آنکه تمامی سیستم های مذکور نقش هدایت و کنترل ماندگار خودرو را بر عهده دارند. بنابراین شناسایی و پیش بینی رفتار تایر خودرو در شرایط مختلف (شتابگیری، ترمزگیری، حرکت در پیچ ها و غیره) از اهمیت ویژه ای در طراحی کنترل کننده های سیستم های هدایت و کنترل خودرو برخوردار است.
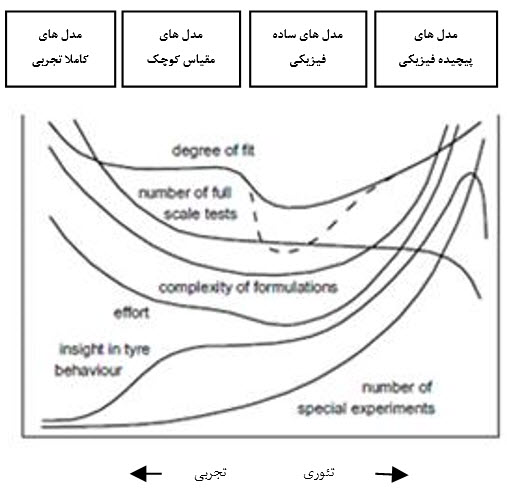
در نیم قرن اخیر مدل های مختلفی توسط پژوهشگران برای تایر خودرو ارائه گردیده است که هرکدام از آنها به منظور تمرکز بر موضوعی خاص طراحی شده و دارای مزایا و معایب متفاوتی می باشند که باید بر حسب نیاز، مدل مورد نظر را انتخاب کرد. پیچیدگی نیروهای وارد بر تایر خودرو به علت ارتباط آن با لغزش های طولی و جانبی و پارامترهایی از قبیل میزان بار عمودی اعمالی به تایر، فشار باد تایر، سرعت خودرو و غیره موجب شده تا پژوهشگران نتوانند مدل کامل و همه جانبه ای در مورد تایر خودرو ارائه دهند. شکل (1) سیر تکاملی و نحوه ی مدلسازی تایر خودرو را نشان می دهد. این شکل می تواند مبنای مناسبی جهت انتخاب مدل مطلوب تاير خودرو با در نظر گرفتن معیارهای مورد توجه طراح باشد[2].
شکل (1): سیر تکاملی و نحوه مدلسازی تایر
با توجه به شکل (1) از دو روش کلی جهت مدلسازی تاير خودرو استفاده شده است. روش های تجربی که در سمت چپ شکل (1) نشان داده شده و روش های تحلیلی و تئوری که در سمت راست شکل (1) قرار گرفته است. در وسط شکل (1) مدل ها عمدتا ساده بوده و دارای دقت کاربردی کمی هستند، در حالیکه در سمت چپ و راست شکل (1)، مدل ها دارای دقت بالاتری می باشند اما از مدل های تحلیلی پیچیده که در سمت راست قرار گرفته اند، معمولا در شبیه سازی دینامیک خودرو استفاده نمی شود.
گروه مدل های تجربی، بر مبنای خصوصیات تایر خودرو و با آزمایشات تجربی بدست آمده است. در این روش نتایج حاصل از آزمایش های تجربی با روابط ریاضی تطابق داده می شوند. در این گروه مشهور ترین مدل، فرمول جادویی (Magic Formula) نام دارد.
گروه مدل های مقیاس کوچک، بر اساس استفاده از خصوصیات اصلی و پایه تایر که نوعا توسط محاسبه بدست می آیند، استوار است. گروه مدل های فیزیکی ساده، وابسته به نوع تایر می باشد. در این گروه روابط ساده و با دقت خوب در محدوده خاصی از عملکرد تایر جوابگو می باشند. یکی از مدل های معروف این گروه، مدل HSRI می باشد که توسط Dugoff و همکاران ارایه شده است. گروه مدل های فیزیکی پیچیده، دارای روابط پیچیده ریاضی بوده و از روش های آنالیز المان محدود حاصل می شوند. این روش ها برای شبیه سازی دینامیک خودرو مورد استفاده قرار نمی گیرند و بیشتر برای فرآیند ساخت، تولید و شناسایی عملکرد تایر در اثر تنش و کرنش مورد استفاده قرار می گیرند.
علاوه بر دسته بندی فوق، از دیدگاه نحوه نیروهای اعمالی به تایر، می توان مدل های تایر را به دو گروه تقسیم کرد.
- استاتیکی
- دینامیکی
مدل های استاتيکی تاير خودرو
یکی از مشهورترین و پرکاربرد ترین مدل های استاتیکی، مدل ارایه شده توسط پسیجکا[2] می باشد که تحت عنوان فرمول جادویی[3] معروف می باشد. این مدل از داده های تجربی استخراج گردیده و بطور کامل نشان دهنده رفتار تایر می باشد. یکی از خصوصیات مدل پسیجکا این است که به طور واحد، بیان کننده نیروی طولی، نیروی جانبی و گشتاور خود تنظیم تایر خودرو می باشد. حالت کلی آن مطابق رابطه (1)می باشد.
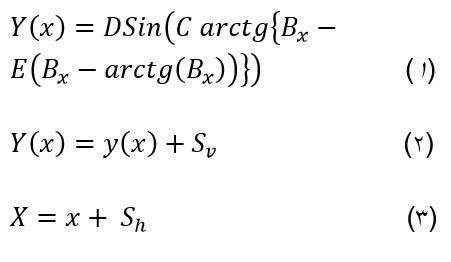
پارامترهای این رابطه عبارتند از:
B: ضریب سختی (stiffness factor)
C: ضریب شکل (shape factor)
D : ضریب پیک (prak factor)
E: ضریب انحنا (curvature factor)
Sh: تغییر افقی( horizental shift)
Sv: تغییر عمودی(vertical shift)
از عوامل تاثیرگذار در رابطه (1) مقدار نیروی عمودی Fz وارد بر تایر و زاویه کمبر تاير خودرو می باشد که در روابط بعدی لحاظ گردیده است.
شکل (2) تغییرات نیروی جانبی (Fy) بر حسب ضریب لغزش جانبی تایر را که از فرمول جادویی پسیجکا بدست آمده است را نشان می دهد.
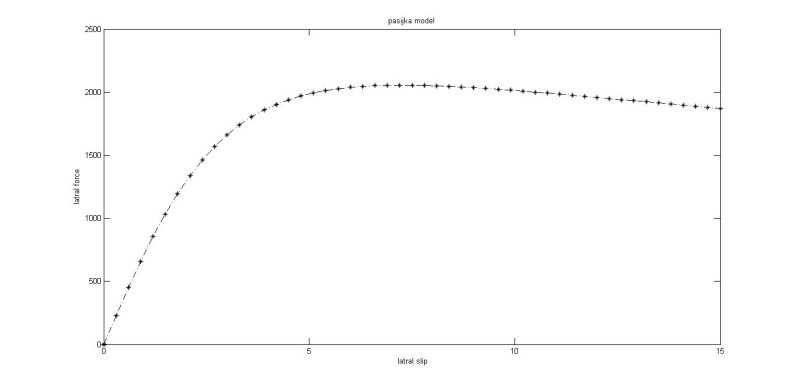
شکل (2): نمودار نیروی جانبی بر حسب ضریب لغزش جانبی
چنانچه رابطه (1) با روابط (4) تا (11) در نظر گرفته شود نیروی جانبی[1]تایر را می توان بدست آورد. [1] The side force
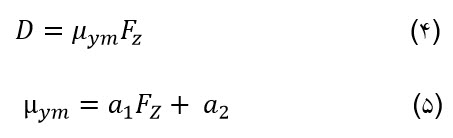
µym : ضریب اصطکاک جانبی
a1 : وابستگی بار عمودی نیروی اصطکاک جانبی
a2 : سطح نیروی اصطکاک جانبی
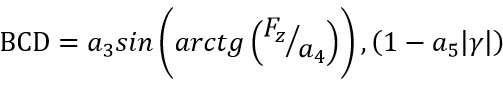
a3: ماکزیمم سختی جانبی در لاندا = 0
a4 : بار عمودی در ماکزیمم سختی جانبی
a5 : حساسیت کمبر سختی جانبی
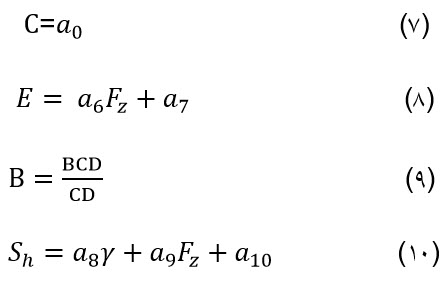

شکل (3): نمودار نیروی جانبی بر حسب لغزش جانبی تحت بارهای عمودی مختلف
شکل (3) نیروی های جانبی وارده بر تایر را بر حسب ضریب لغزش جانبی در شرایط مختلف اعمال بار عمودی نشان می دهد.
با در نظر گرفتن رابطه (1) با روابط (12) تا (18) نیروی طولی[1] تایر بدست می آید. [1] longituadinal force
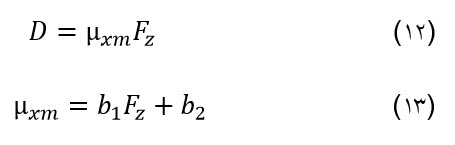
µxm : ضریب اصطکاک طولی
b1 : ضریب وابستگی بار عمودی برای نیروی اصطکاک طولی
b2 : سطح نیروی اصطکاک طولی
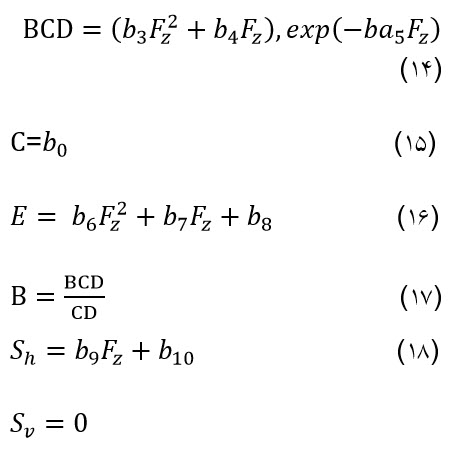
شکل (4) نیروی طولی وارده بر تاير خودرو را بر حسب ضریب لغزش طولی در جاده های مختلف دارای ضرایب اصطکاک متفاوت را نشان می دهد.
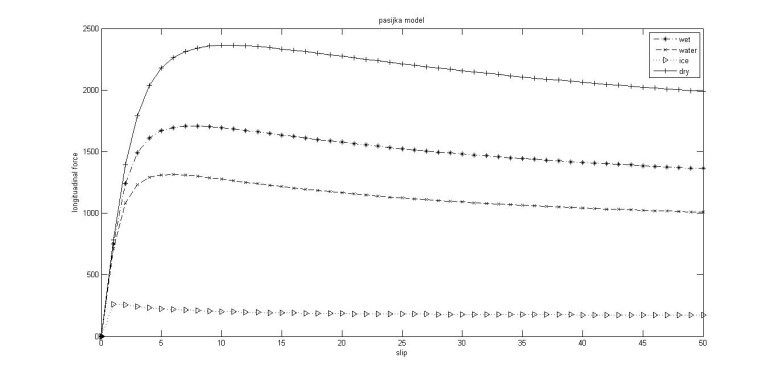 شکل (4): نیروی طولی حاصل از مدل پسیجکا در جاده های مختلف
شکل (4): نیروی طولی حاصل از مدل پسیجکا در جاده های مختلف
با ترکیب رابطه (1) با روابط (19) تا (25) نیز می توان گشتاور خود تنظیم چرخ را بدست آورد:
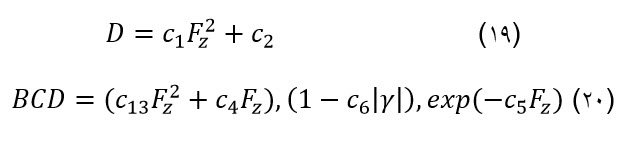
C6: حساسیت کمبر سختی تنظیم کننده
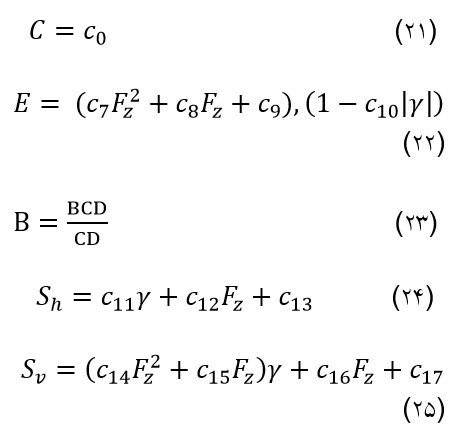
از خصوصیات این مدل می توان به موارد زیر اشاره کرد:
1. تطابق نزدیک نمودار حاصل از مدل با داده های تجربی
2. قابلیت نمایش تمام خصوصیات فضای حالت تایر
3. دارای معنی فیزیکی بدین مفهوم که می توان با تغییر پارامترهای فیزیکی موثر در تایر، نتایج حاصل را بررسی کرد
4. ساده و مختصر بودن
5. دقت بالا
مدل دیگر ارائه شده از نوع مدل های استاتیکی مدل Buckhardt می باشد. در این مدل ضریب اصطکاک بین تایرخودرو و جاده تابعی بر حسب لغزش و سرعت خودرو می باشد. [4]

که پارامترهای آن عبارتند از:
C1 : حداکثر مقدار منحنی اصطکاک
C2 : پارامتر مربوط به شکل منحنی اصطکاک
C3 : تفاوت بین حداکثر ضریب اصطکاک و مقدار ضریب اصطکاک به ازای λ=1
C4 : مقدار مشخصه رطوبت، که عددی بین 0.02 – 0.04 m/s است.
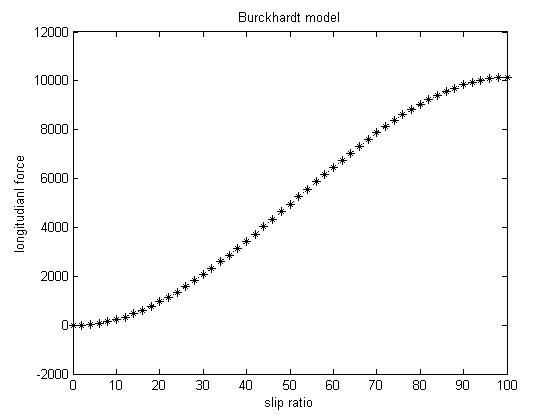
شکل (5): نمودار نیروی طولی حاصل از مدل Burckhardt
شکل (5) نیروی طولی بر حسب ضریب لغزش با شرایط کاهش خطی سرعت، از m/s 15 به m/s 5 و افزایش ضریب لغزش طولی از 0 تا 100 در مدت زمان 10 ثانیه را نشان می دهد.
Daiss , kienke مدل Burckhardt را با صرف نظرکردن از سرعت خودرو(ν)، ساده سازی کرده اند که جزئیات آن نیز در مرجع [5] آمده است.
تمامی مدل های ارایه شده در بالا غیر خطی بوده و دارای پارامترهایی است که شناخت و اندازه گیری آنها مستلزم استفاده از اطلاعات تجربی بدست آمده از به کار بردن تجهیزات آزمایشگاهی ویژه می باشد. این در حالی است که این مدل ها در مورد سیستم های خطی پاسخ مناسب را ارایه نمی کنند.
Carlos canudas و همکاران مدل زیر را ارایه کرده اند: [6]
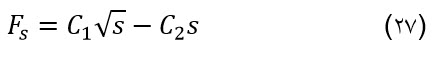
نکته مهم در مورد ضرایب ثابت معادلات بالا این است که این ضرایب کاملا ثابت نبوده و تحت تاثیر خصوصیات تایر مانند ترکیبات، نوع گام (tread type)، ارتفاع گام(tread depth)، فشار باد تایر، دما و خصوصیات جاده از جمله نوع سطح، پوشش، آبریزگاه، ظرفیت بار، مقدار چرب شدگی و همچنین شرایط خودرو از جمله سرعت و بار می باشند. [7]
مدل های ديناميکی تاير خودرو و زمين
مدل های اصطکاکی استاتیکی در فضای حالت در شرایط خطی و سرعت های زاویه ای مورد استفاده قرار می گیرند و در حقیقت از داده های تجربی حاصل از تجهیزات خاص که امکان تغییر سرعت خطی و زاویه ای را می دهند، بدست می آیند. در مقابل مدل های استاتیکی، مدل های دینامیکی ارایه شده اند که تحت عنوان کلی “ Dynamic Friction models “ شناخته می شوند. این مدل ها بیان کننده رفتار واقعی تایر در زمان تغییر سرعت می باشند و به دو دسته کلی متمرکز و گسترده تقسیم می شوند. [8]. [8] Dynamic slip/force models
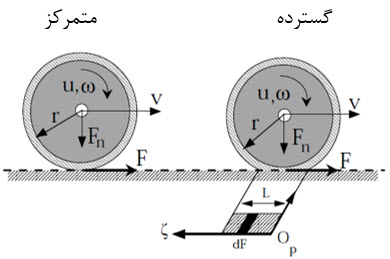
شکل (6): مدل دینامیکی متمرکز و گسترده تاير خودرو[6]
مدل متمرکز که در شکل (6) سمت چپ نشان داده شده است، یک نقطه را به عنوان نقطه تماس تاير خودرو و جاده در نظر می گیرد و در نتیجه معادله بدست آمده با انتگرال گیری از معادله نسبت به زمان قابل حل می گردد. در عوض، مدل گسترده، سطح گسترده ای را برای تماس تاير خودرو با جاده در نظر می گیرد و توزیع فشار را بصورت یکنواخت فرض می کند و برای حل کردن معادله نسبت به زمان و فضا باید از آن انتگرال گرفت.
Bliman و همکاران[9] روابطی را از حل معادله دیفرانسیلی شبیه به رابطه (28) بدست آورده است.
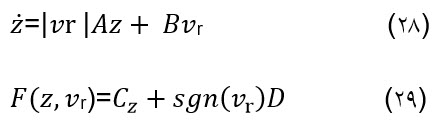
مدل های Dahl وkinematic نیز مدل هایی از رفتار دینامیکی تایر را ارایه می کنند که در مقایسه با فرمول جادویی، رفتار تایر را واقعی تر نشان می دهد اما مدل دیگری تحت عنوان لوگری (LuGre ) ارایه گردیده که بسیاری از محققان استفاده از آن را پیشنهاد کرده اند.[6]
مدل لوگری که توسعه داده شده مدل Dahl می باشد بصورت یک معادله دیفرانسیل مطابق رابطه (29) بیان می شود. در این مدل نیروها و سطح تایر به طور متمرکز در نظر می گیرند. مدل لوگری بوسیله روابط (30) تا (32) بیان می شود. [10]
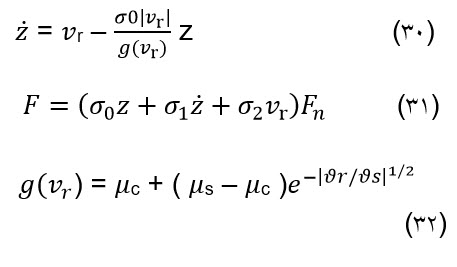
که پارامترهای آن عبارتند از:
سیگما 0: ضریب سختی متمرکز طولی نرمالیزه شده لاستیک
سیگما 1 : ضریب دمپ متمرکز طولی نرمالیزه شده لاستیک
سیگما 2 : ضریب دمپ ویسکوز نرمالیزه شده
مو c : ضریب اصطکاک کلمب نرمالیزه شده
مو s : ضریب اصطکاک ایستایی نرمال شده
Fn : نیروی عمودی
z : وضعیت اصطکاک داخلی
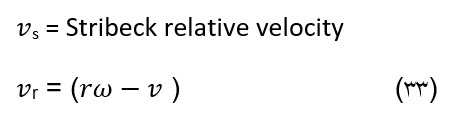
r= شعاع چرخ
w= سرعت زاویه ای چرخ
v= سرعت خطی خودرو
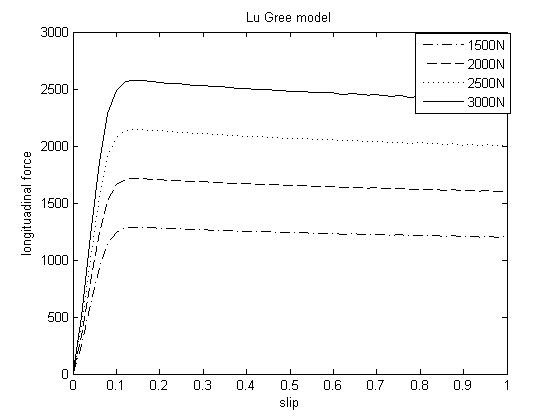
شکل (7): نیروی طولی وارده بر تایر تحت بار عمودی مختلف
شکل (7) نشان دهنده نیروی طولی حاصل از مدل لوگری تحت تاثیر بارهای عمودی مختلف را نشان می دهد.
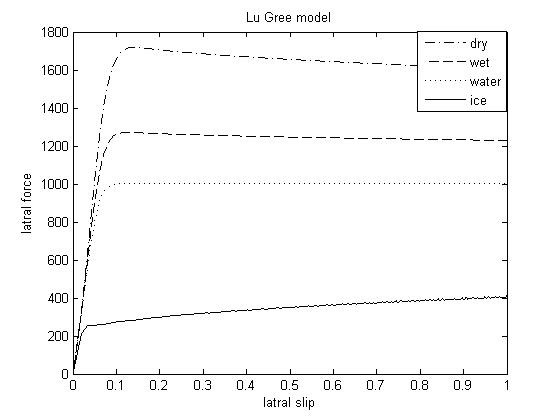
شکل(8): نیروی طولی وارده بر تایر تحت بار عمودی مختلف
شکل (8) نشان دهنده نیروی طولی وارد بر تاير خودرو تحت شرایط مختلف جاده را نشان می دهد.
مدل Brush
یکی از مدل هایی که تایر خودرو را بصورت دینامیکی و با استفاده از روش های فیزیکی مدل سازی می کند، مدل brush می باشد. در این مدل سطح تایر به المانهای کوچکی تقسیم شده و با توجه به میزان نرخ لغزش، نیروی وارده بر تایر بدست می آید.
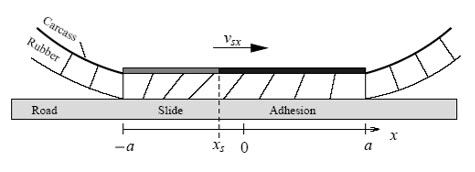
شکل (9): تغییر شکل لاستیک در محل تماس با جاده مطابق با مدل brush. المان های تایر با سرعت vsx متناسب با جاده حرکت می کند. منطقه تماس با سرعت حرکت خودرو vx حرکت می کند.[12]
همانطور که در شکل (9) ملاحظه می شود، مدل brush، تایر را به المان های کوچک عمود بر سطح جاده تقسیم می کند به طوریکه این المان ها در سطح تماس بین تایر و زمین دارای زاویه های متفاوتی می باشند. این قسمت به دو ناحیه چسبندگی (Adhesion) و لغزش (slide) تقسیم می شود. برای شروع تحلیل و نوشتن روابط، یک المان در زمان t=0 و x=a تعریف می گردد.
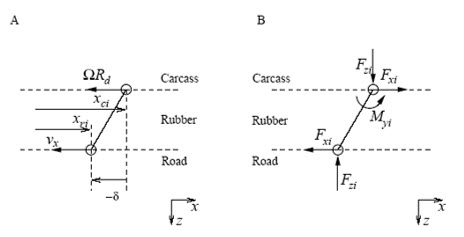
شکل (10): سینماتیک و دینامیک المان های لاستیک بین بدنه ی تایر و جاده [12]
در شکل (10) حالت A ارتباط بین سرعت و موقعیت یک المان که در نقطه بالایی بر روی قالب تاير خودرو و در نقطه پایینی بر روی سطح جاده قرار گرفته است، را نشان می دهد. در قسمت B نیروهای وارد بر المان مذکور نشان داده شده است.
موقعیت این نقاط در صورت عدم وجود لغزش بصورت زیر تعریف می گردد.

a2: طول تماس تایر با زمین
Ω: سرعت دورانی تایر
Rd: شعاع دینامیکی چرخ
Vx : سرعت خودرو
تغییر شکل المان عبارت است از:

اگر سرعت ها ثابت در نظر گرفته شوند، از ترکیب روابط (34) تا (36) رابطه (37) بدست می آید.
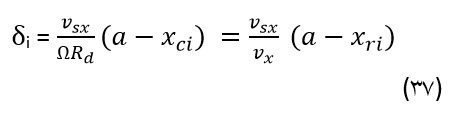
که عبارت sx /Ω Rdν مقدار لغزش طولی نامیده می شود و با سیگما x نشان داده می شود.
تاير خودرو الزاما بصورت خطی تغییر شکل نمی دهد، اما می توان تغییرات آن را بصورت خطی فرض کرد. مقدار نیرویی که برای شروع و رسیدن به تغییر شکل لازم می باشد، می توان از رابطه (38) بدست آورد.

k : ضریب ثابت
تغییر شکل المان های تایر بوسیله اصطکاک بین تایر و زمین محدود بوده و مقدار ماکزیمم نیروی عمل کننده بر روی المان از طریق رابطه (39) قابل محاسبه می باشد:

از ترکیب (38) و (39) ماکزیمم مقدار تغییر شکل مطابق رابطه (40) بدست می آید.

المان زمانی شروع به لغزش می کند که مقدار تغییر شکل به مقدار ماکزیمم خود برسد. در این صورت نیروی عمل کننده بر روی المان های تایر معادل رابطه (38) می باشد. با توجه به نیروهای اعمال شده به المان های تایر میزان چسبندگی تایر به جاده و لغزش تایر، سه حالت زیر ایجاد می شود.
- چسبندگی کامل. در این حالت منحنی لغزش فقط به خصوصیات تایر وابسته است.
- هم لغزش و هم چسبندگی. در این وضعیت سطح تماس به دو قسمت تقسیم می شود، یک قسمت چسبندگی و قسمت دیگر در حال لغزش.
- لغزش کامل. در این حالت نیروی ترمزی تنها به مقدار ضریب اصطکاک در شرایط واقعی وابسته است.
زمانی که هم چسبندگی و هم لغزش اتفاق می افتد، محاسبه موقعیت المان در زمان آغاز لغزش امکان پذیر می باشد که نقطه Breakaway نامیده می شود. با استفاده از معادلات (37) و (40)، رابطه (41) بدست می آید:
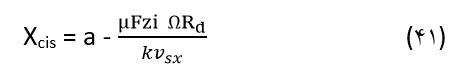
با انتگرال گرفتن بر روی تمامی طول تماس و با در نظر گرفتن مقدار k برابر با Cp dxc ، Fzi = qz(xc) dxc حاصل می گردد. در اینجا cp مقدار سختی در واحد طول و qz مقدار نیروی عمودی بر واحد طول بین تاير خودرو و زمین می باشد. علاوه بر آن نیروی حاصل از چسبندگی سطح و همچنین نیروی حاصل از منطقه لغزش، تمامی نیروی ترمزی را مطابق رابطه (42) ایجاد می کند.
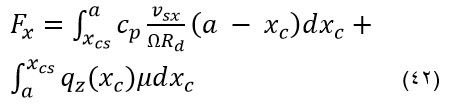
فرمول (42) را می توان با استفاده ازXr و Xc نیز نوشت. نیروی عمودی بصورت بار گسترده بر روی تمام طول المان بصورت Fzi=qz(xci) در نظر گرفته می شود. همچنین Xr می تواند جایگزین Xc گردد. (البته زمانی که تقسیم فشار یکسان در بین تایر و زمین تعریف شده باشد). فاصله المانهای در نظر گرفته شده در بالای سطح تماس تایر با زمین یکسان بوده اما، فاصله های المان ها در سطح تماس متغیر می باشند. بنابراین نمی توان کران های مناسبی برای انتگرال گرفتن مناسب بدست آورد. بنابراین از این بعد اندیس c را حذف می کنیم و x موقعیت قالب تایر را نشان می دهد.
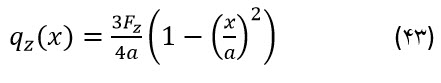
این موقعیت در شکل(11) نشان داده شده است.
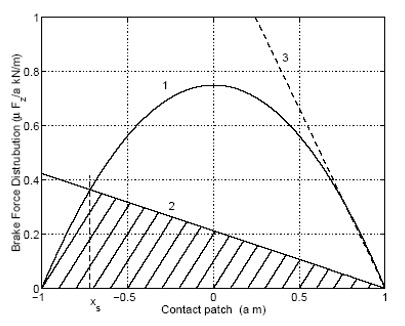
شکل (11): تغییر شکل لایه لاستیک بین محل تماس تایر و زمین را نشان می دهد. [12]
منحنی شماره 1 مقدار ماکزیمم نیروی ترمزی در دسترس در واحد طول که برابر با (µqz(x می باشد، را با توجه به توزیع نیروی ترمزی نشان می دهد. منحنی شماره 2، نیرو در واحد طول لازم برای تغییر شکل الیاف لاستیکی، متناسب با سرعت های مختلف را نشان می دهد. ناحیه هاشور خورده مقدار نیروی کل حاصل از تغییر شکل المان را نشان می دهد. اگر سطح تماس فقط دارای چسبندگی باشد قسمت هایی از تایر دچار لغزش نیز می شوند.
مختصات نقطه شکست xs را می توان از رابطه (44) بدست آورد:
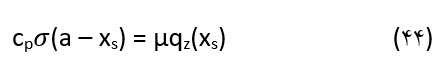
با در نظر گرفتن رابطه (42) و توزیع فشار ناشی از رابطه (43)، رابطه (45) بدست می آید که می توان مقدار نیرو را بدست آورد.
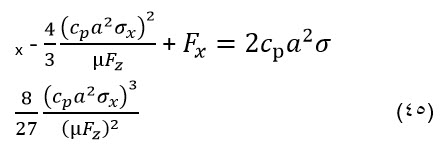
با توجه به رابطه (45) مقدار لغزش به خصوصیات تایر در نرخ های لغزش کوچک وابسته است. اغلب، در این منطقه، رابطه بین لغزش-نیرو با ضریب اصطکاک بصورت خطی فرض شده است و Cx نامیده می شود که از طریق رابطه (46) محاسبه می گردد.
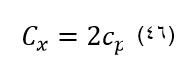
در لغزش های بزرگتر، ضریب اصطکاک مهمترین منبع برای تعیین خصوصیات می باشد. اگر شیب خط 2 تندتر از شیب خط 1 در x=a شود، با توجه به شکل (11) حالت لغزش کامل اتفاق می افتد که این شیب با خط 3 نشان داده شده است. شیب توزیع نیروی ترمزی در x=a در جایی که تمام سطح تاير خودرو شروع به لغزش می کند، در شیب محدودی قرار می گیرد که از رابطه (47) قابل محاسبه می باشد:

برای لغزش های بسیار زیاد، مقدار نیروی ترمزی از رابطه (48) حاصل می شود.

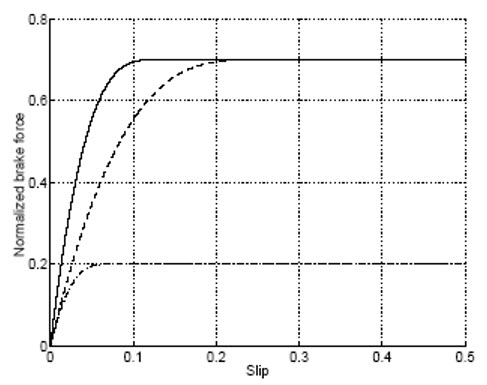
شکل (12): نیروی ترمزی نرمال شده مستخرج از مدل براش [12]
شکل (12) نیروی ترمزی نرمالیزه شده در لغزش طولی با استفاده از مدل براش برای ضریب اصطکاک های مختلف و سختی های لاستیک متفاوت نشان می دهد.
نيرو های تاير
تایر خودرو نیروهای مختلفی از جمله نیروی عمودی حاصل از وزن خودرو، نیروی های جانبی حاصل از تغییر جهت خودرو و نیروهای آئرودینامیک را توسط سطح تماس خود به زمین منتقل می کند. به طور کلی تایر عهده دار چهار وظیفه اصلی به شرح زیر می باشد.[11]
1.جذب ضربات ناشی از ناهمواریهای جاده
2.تحمل نیروهای عمودی
3.ایجاد و بهبود نیروهای طولی جهت شتابگیری و ترمز گیری
4.ایجاد و بهبود نیروی جانبی برای تغییر جهت خودرو
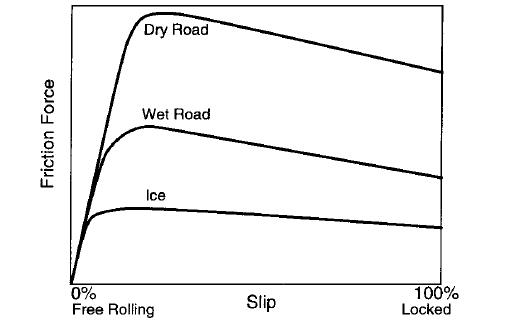
شکل (13): نمودار نیروی طولی وارده بر تایر نسبت به ضرایب مختلف [11]
شکل (13) نشان دهنده نیروهای طولی وارده به تایر در جاده های مختلف را در شرایط واقعی نشان می دهد. عوامل مختلفی از جمله فشار باد تایر و بار نرمال بر روی مشخصات عملکردی تایر تاثیر می گذارند، این تغییرات عمدتا غیر خطی بوده و چنانچه از محدوده مجاز تجاوز کند باعث عملکرد نامطلوب تایر خواهد شد.
مقايسه مدل های استاتيکی و ديناميکی
مدل های استاتیکی و دینامیکی ارائه شده در بالا دارای ورودی های مختلف، دقت های متفاوت و همچنین سادگی و پیچیدگی های خاص خود می باشند. مدل پسیجکا تحت تاثیر ضریب لغزش تایر، نیروی عمودی وارد بر تایر، ضریب اصطکاک بین تاير خودرو و زمین و زاویه کمبر چرخ می باشد. که نیروی طولی در راستای چرخ که در شکل (3) آمده است، با استفاده از نرم افزار سیمولینک MATLAB که قسمتی از برنامه در شکل (14) ملاحظه می گردد، شبیه سازی گردیده است.
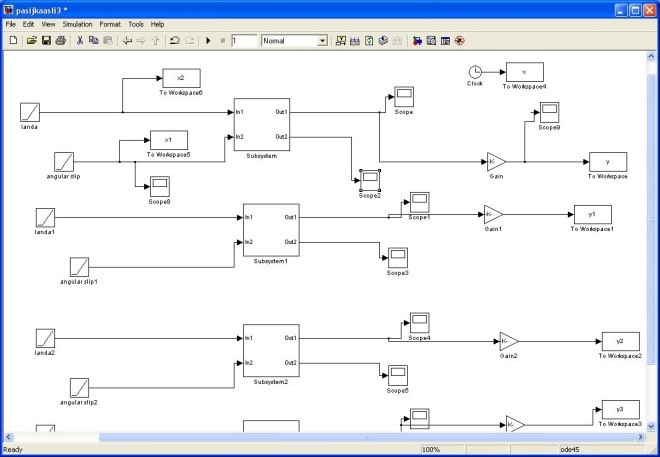
شکل (14): قسمتی از برنامه شبیه سازی مدل های مختلف تایر در سیمولینک Matlab
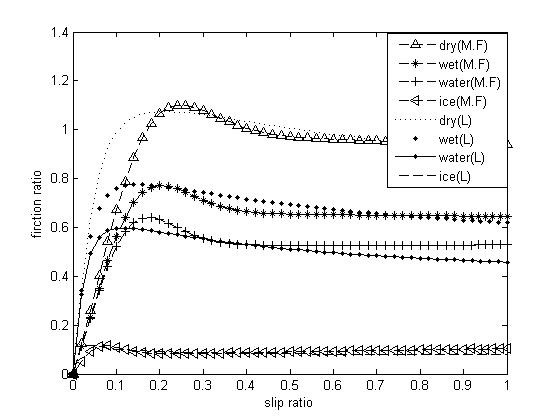
شکل (15): نیروی نرمالیزه شده طولی وارده بر تایر در دو مدل پسیجکا (M.F) و لوگری (L)
با استفاده از مدل Buckhardt ضریب اصطکاک بین تایر و جاده که تابعی بر حسب لغزش و سرعت خودرو می باشد، را می توان بدست آورد. این مدل ساده تر از مدل های دیگر بوده و دارای دقت کمتری نسبت به پسیجکا می باشد.
مدل لوگری، تایر را بصورت دینامیکی مدل می کند و تحت تاثیر ضریب اصطکاک بین تایر و زمین، نیروی عمودی وارد بر تایر، سرعت خطی و سرعت زاویه ای تایر می باشد که دارای تطابق بسیار خوبی با رفتار واقعی تایر دارد.
شکل (15) نتایج حاصل از مدل سازی تایر با استفاده از مدل لوگری و پسیجکا را نشان می دهد. این شکل که نیروهای طولی نرمالیزه شده در دو مدل فوق را نشان می دهد مبین این نکته است که مدل های مذکور تطابق نسبتا خوبی با یکدیگر و بصورت کلی با نمودار مرجع شکل (13) دارند.
با توجه به شکل (15) ملاحظه می گردد که مدل لوگری رفتار واقعی تایر را بهتر مدل می کند، و این موضوع در مقالات متعددی از جمله [6] ذکر شده است
مدل ارایه شده توسط brush تحت تاثیر مقدار نیروی عمودی وارده بر واحد طولqz ، ضریب سختی لاستیک Cp و ضریب اصطکاک بین تایر و زمین می باشد. Cp وابسته به خصوصیات مواد تشکیل دهنده لاستیک از جمله ضخامت لاستیک، دما و سن می باشد. مقدار سطح تماس بین تایر و زمین عامل تاثیرگذار دیگری است که خود به فشار درونی تایر و بار وارده به چرخ Fz بستگی دارد. ضریب اصطکاک مقداری ثابت نبوده و با توجه به نوع جاده، شرایط رانندگی و لغزش تایر بر روی جاده متغیر خواهد بود. از مزیت های این مدل می توان به سادگی آن اشاره کرد.
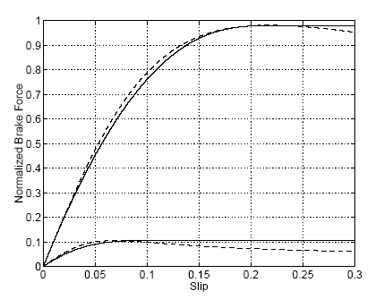
شکل(16):مقایسه مدل براش و مدل پسیجکا [12]
شکل (16) نیروی جانبی حاصل از دو مدل مدل براش(خط پیوسته) و پسیجکا (خط چین)، در جاده های مختلف را با هم مقایسه می کند که از روی تایر واقعی بدست آمده است. همانطور که در شکل نشان داده شده است، دو مدل با یکدیگر تطابق خوبی دارند اما در اندازه گیری های انجام شده در آزمایش ها، فرمول جادویی دقیقا خصوصیات فرض شده تایر را پوشش نمی دهد. تفسیر اینکه مدل brush تطابق بهتری با رفتار واقعی تایر دارد نیز شاید درست نباشد. در این مدل تخمین ضریب اصطکاک در لغزش های کم در مقایسه با لغزش های بزرگتر، تطابق بهتری با واقعیت دارد.
نتیجه گیری:
مدل های تایر ارائه شده توسط پژوهشگران دارای تنوع زیادی بوده که هرکدام بنا به دقت و پیچیدگی از سطوح مختلفی برخودارند. سه مدل لوگری، مدل پسیجکا و مدل براش از سایر مدل ها بیشتر مورد استفاده قرار می گیرد. انتخاب اینکه کدام مدل رفتار واقعی تری از تایر را ارایه می کند، چندان ساده نمی باشد. زیرا پیچیدگی نیروهای وارد بر تایر به علت ارتباط آن با لغزش های طولی و جانبی و پارامترهایی از قبیل فشار باد تایر و سرعت خودرو موجب شده تا پژوهشگران نتوانند نظریه کاملی در مورد تایر ارایه دهند. لذا پژوهشگران باید با توجه به نیاز طراحی، دقت و میزان پیچیدگی مدل مناسب را انتخاب نماید. با مقایسه نمودار های خروجی نیروی طولی وارد به تایر می توان دريافت که مدل لوگری تطابق بهتری با رفتار واقعی تایر در جاده های مختلف دارد.در مقالات متعددی از جمله منبع [6] نيز به برتری مدل لوگری بر سایر مدل ها تاکید شده است.
منابع:
[1] : سید محسن نوایی ، کاظم مقدمیان، “تایر، انتخاب، استفاده، نگهداری”نشر رزقی، 1389، صفحه 7
[2]: [1] Hans B. Pasijka “ tyre and vehicle dynamics” second edition; Butterworth-Heinemann is an imprint of Elsevier,2006 pg . 85
[3]: Egbert Bakker . Hans B. Pasejka , Lars Lidner , “ A new tire model with an application in vehicle dynamic studies” SAE, p 890087
[4]: Ming-chin Wu, Ming-chang Shih, “Simulated and experimental study of hydraulic anti-lock braking system using sliding-mode PWM control”, Department of Mechanical Engineering, National Cheng Kung University, Tainan, Taiwan, ROC, 2001 Mechatronics 13 (2003) 331–351
[5]: A Diass & U. Kinck , “ Estimation of tyre slip during combined cornering and braking observer supported fuzzy estimation “ , 13th triennal world congress span Francisco, pp 41-46 ,1996
[6]: Carlos Canudas-de-Wit, Panagiotis Tsiotras†, Efstathios Velenis, Michel Basset and Gerard Gissinger, “Dynamic Friction Models for Road/Tire Longitudinal Interaction”, Vehicle System Dynamics,2002
[7]: Pasterkamp , WR. And Pasejka , H .B.” the tire as a sensor to estimate friction “ , vehicle system dynamics, vol 29 pp 409-422, 1977
[8]:carlos canudas de wit , panagiotis tsiotras ,”dynamic tire friction models for vehicle traction control”,USA, 2002
[9]: Bliman P.A. , Bonald , T . and Sorine , M. , “ Hysteresis operators and tire friction models : application to vehicle dynamic simulation. “ Proc. of ICIAM 95,Humburg , germany , 1995
[10]: Canudas de Wit, C., Horowitz, R. And Tsiotras, P., “ Model-Based Observer for Tire/Road Contact Friction Prediction,” In new Direction in nonlinear Observer Design , Nijmeijer, H. And T.I Fossen (Eds),Springer Verlag , May 1999
[11]: Thomas D. Gillespi,”Fundamentals of vehicle Dynamics”,ASE , pg.344
[12]: Jacob Svendenius_, BjörnWittenmark,” BRUSH TIRE MODEL WITH INCREASED FLEXIBILITY” ,Haldex Brake Products AB, Box 501, SE-261 24 Landskrona, Sweden,
نویسندگان: صیاد نصیری
محمد عارف نیا
گروه فنی مهندسی اِیمِگ






